Algorytm a program
Algorytmy to dokładny opis sposobu postępowania prowadzącego do określonego wyniku.
Na przykład algorytm otwierania drzwi: aby otworzyć drzwi, włóż klucz do zamka, przekręć w prawo do oporu a następnie naciśnij klamkę.
Czym różni się algorytm od programu? Programy które tworzy programista są zawsze przeznaczony do wykonania przez automat (komputer). Musi więc być szczegółowy i wyrażony w instrukcjach dla automatu (lub w sposób możliwy do przetłumaczenia na takie instrukcje).
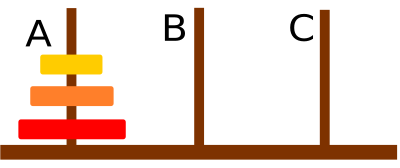
Objaśnimy to na przykładzie łamigłówki „Wieże Hanoi” (https://pl.wikipedia.org/wiki/Wieże_Hanoi). Zadaniem jest na przełożeniu krążków z pierwszego na trzeci słupek zgodnie z regułami:
za każdym razem jeden;
nie wolno kłaść większego krążka na mniejszy
Jeśli nie masz takiej zabawki – można skorzystać z któregoś z dostępnych w internecie programów. Na przykład Przetestujmy:http://www.zagraj.republika.pl/hanoi.html
Jak wykonać to zadanie?
Przekładamy najmniejszy klocek na ostatni słupek, potem średni na środkowy i na nim ten najmniejszy. Mamy w ten sposób dwa mniejsze klocki na środkowym słupku.
Teraz największy kładziemy na ostatnim słupku, najmniejszy na zwolniony pierwszy słupek.
Układamy mniejsze klocki na ostatnim słupku w odpowiedniej kolejności.
Dla człowieka taki opis jest wystarczający. Rozwiązaliśmy zagadkę – pisząc odpowiedni algorytm. Ale przecież żadna maszyna tego nie zrozumie!
Jak przekazać ten algorytm automatowi? Ten automat (program) musi mieć odpowiednie ku temu możliwości: interfejs z możliwością wydawania komend.
Takie środowisko stanowi program dostępny na stronie (wymagany w przeglądarce Flash):
http://otwartaedukacja.pl/programowanie/hanoi/
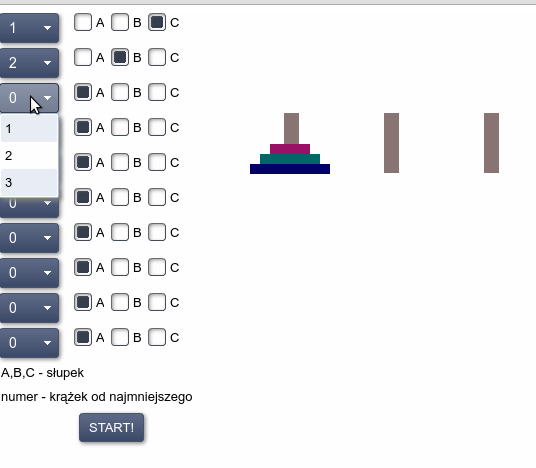
Słupki zostały oznaczone literami A,B,C a krążki cyframi 1,2,3 (od najmniejszego). Zapis 2-B oznacza przełożenie średniego (2) krążka na słupek środkowy (B).
Powyższy algorytm możemy zapisać w tabelce:
Opracowujemy plan działania:
| Lp | działanie |
|---|---|
| 1 | 1-C |
| 2 | 2-B |
| 3 | 1-B |
| 4 | 3-C |
| 5 | 1-A |
| 6 | 2-C |
| 7 | 1-C |
W ten sposób napisaliśmy program dla naszego symulatora wież hanoi!
Przełożenie algorytmu na język komend (napisanie programu) nazywa się implementacją algorytmu.
Pamiętaj: układanie algorytmów może być trudne, ale programowanie (implementacja algorytmów) jest zazwyczaj łatwa.
Grafika żółwia
Instrukcje programów mogą być zapisywane w różny sposób.Powyżej (Wieże Hanoi) był to zbiór par: (numer klocka, litera oznaczająca słupek). W jednym z wcześniejszych przykładów –były to klocki sterujące ruchem żółwia.
Wróćmy dotego przykładu, aby objaśnić kilka konstrukcji stosowanych w programowaniu.
1. Zmienne
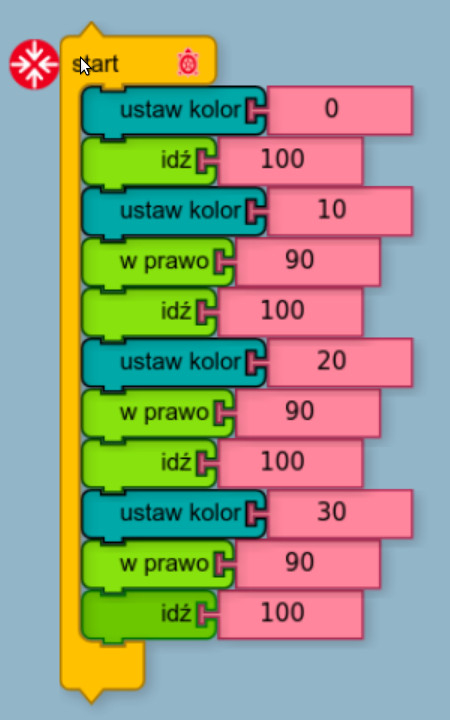
Zmienne w programie http://otwartaedukacja.pl/programowanie/turtle/ zostały nazwane „pudełkami” („boxes”). Są one oznaczane jasnobrązową barwą. Utworzenie pudełka (zmiennej) wykonujemy przez przeciągnięcie i puszczenie klocka „przechowaj w”. Następnie klikamy w nazwę „zmiennej” (domyślnie „pudło”) i wpisujemy dowolny wyraz. Na przykład „barwa”.
Tak utworzoną zmienną (pojawi się w zakładce pudełek) możemy użyć tak jak liczb. Czyli wstawiając ją do zmiennej przechowującej kolor dokonujemy zmiany koloru na taki, jaki mamy zapamiętany w zmiennej „barwa”. Objaśnia to poniższy przykład:
 |
Zastosowanie zmiennej / pudełka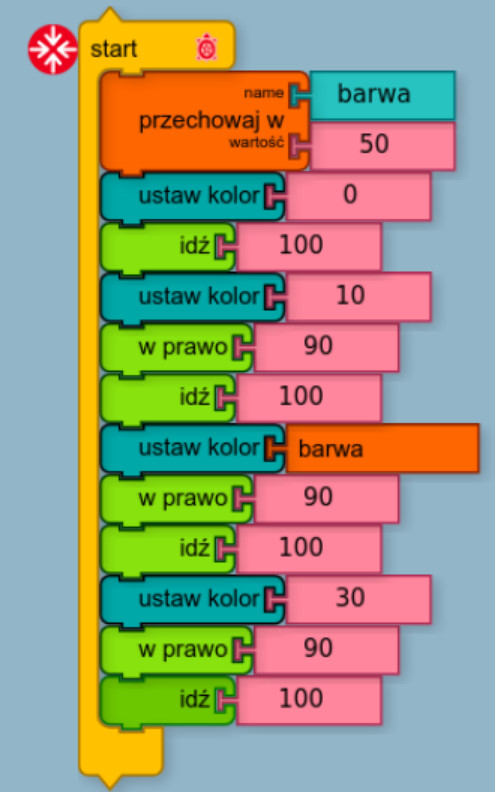 |
|---|---|
Aktualny kolor także jest pamiętany w zmiennej, ale nie jest ona wyświetlana. Wykonując operację „ustaw kolor” zmieniamy tą zmienną.
2. Powtórzenia
Aby narysować kwadrat, musimy powtórzyć cztery razy: narysować bok i obrócuć żówia o kont prosty. Nie musimy tego opisywać czterokrotnie. Dysponujemy klockiem powtórzeń - w zakładce oznaczonej dwoma zawiniętymi strzałkami.Przesuwamy taki klocek (brązowy). Ilość powtórzeń jest domyślnie ustawiona na 4.
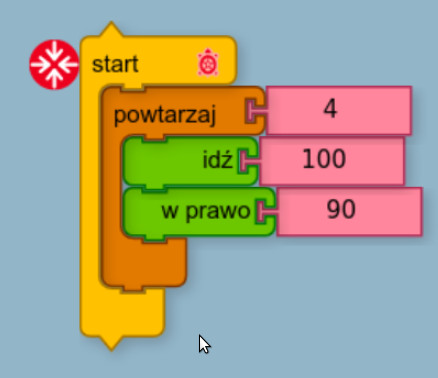
Powtórzenia nazywa się w językach programowania pętlami.
3. Funkcje
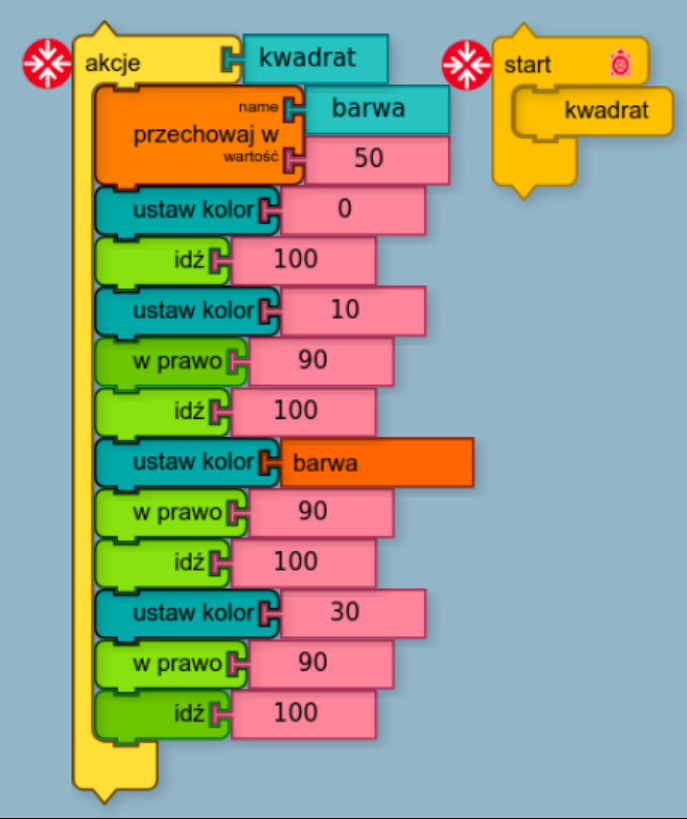
Funkcjami nazywa sięfragmenty programu oznaczone nazwą.W programie z grafiką żółwiafunkcje zostały nazwany określeniem „akcje”iznajdują sięw zakładce otwieranej ikonką zżółtym klockiem.Zdefiniujmy dla przykładu akcję „kwadrat” - przesuwając do niejinstrukcje drukowania kwadratu.
Po zdefiniowaniu (zmianie nazwy) w zakładce akcji pojawia się klocek „kwadrat”, który możemy użyć w miejsce całej sekwencji działań (klocek „start”).
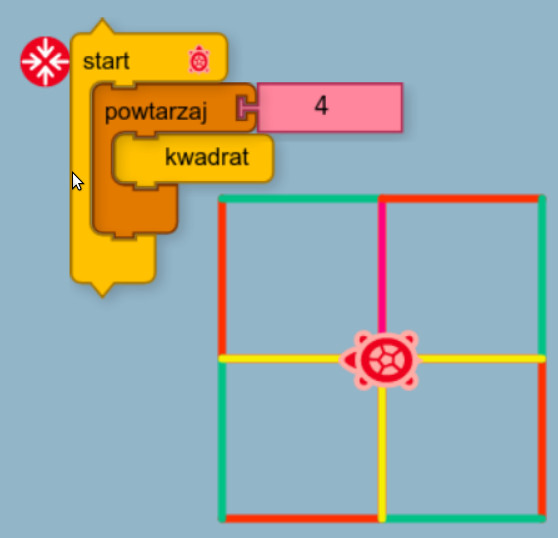
Wszędzie gdzie pojawi się klocek „kwadrat” zastępuje on całą sekwencję działań.Jeśli ta sekwencja (rysowanie kwadratu) ma się pojawić tylko raz – to zastosowanie akcji nie jest wielkim uproszczeniem.
Akcje możnaoczywiście użyć także w powtórzeniach:
Blockly – programowanie wizualne
Bloczki użyte w programie sterującym żółwiem pochodzą z projektu Blockly firmy Google https://developers.google.com/blockly/. Na bazie tego programu powstało wiele ciekawych gier i systemów programowania (zobacz: https://blockly-games.appspot.com/).
Pod adresemhttp://www.otwartaedukacja.pl/programowanie/bl/code/ przygotowano taki graficzny edytor programów, który wykorzystuje projekt Blocky rozwijany przez Google. Pomaga on w nauce programowania. Programy można układać tak jak układa się klocki Lego.
Weźmy na przykład Algorytm Euklidesa (starożytny matematyk grecki Euklides zauważył, że największy wspólny podzielnik dwóch liczb nie zmienia się, gdy od większej odejmiemy mniejszą).
Jego implementacja w postaci klocków może wyglądać następująco:
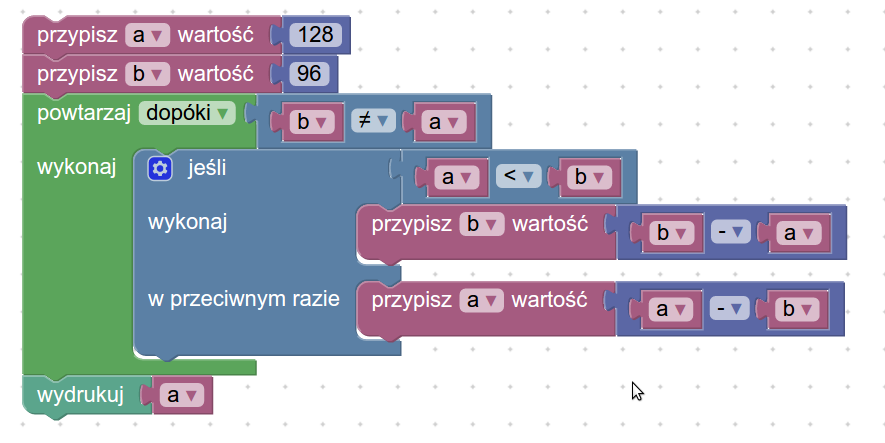
Ten portal umożliwia między innymi generowanie kodu w różnych językach programowania. Na przykład w języku Python. Wśród bloczków nie ma operacji pobierania danych. Po ich dopisaniu (dwie pierwsze linijki - w miejsce zainicjowania konkretnymi liczbami) uzyskamy program:
a=int(input('liczba a='))
b=int(input('liczba b='))
while b != a:
if a < b:
b = b - a
else:
a = a - b
print(a)
Słowo „while” oznacza powtórzenia (tu: póki a jest różne od b). Instrukcja if … else oznacza warunek: jeśli (a<b) to …. a w przeciwnym wypadku (else) ….
Zapis int() oznacza wprowadzanie liczby całkowitej, input() odczyt tego co użytkownik komputera pisze na klawiaturze, a napisy (łańcuchy znaków) 'liczba ...=' - co się wyświetli przed pobraniem danych.
Programowanie w Pythonie
Porównując przejrzystość zapisu schematów blokowych, bloczków, programu w Pythonie, dyskusyjne wydaje się twierdzenie, że reprezentacja graficzna jest lepsza. Na pewno nie jest tak w przypadku złożonych programów.
Dlatego warto rozważyć połączenie nauki programowania z poznawaniem języka Python. Takie założenie przyjęte zostało przy redagowaniu podręcznika programowania w Pythonie: http://wydawnictwo.galicea.org/pyprog
Proste programy z tego podręcznika można próbować na stronie: http://python.otwartaedukacja.pl/
W naturalnym przejściu od grafiki żółwia do programowania w Pythonie może pomóc program Blockpy: http://otwartaedukacja.pl/programowanie/bl/py/. Zawiera on taki sam edytor graficzny (Blockly) zintegrowany z interpreterem Pythona (programem wykonującym napisane w Pythonie programy). Wykorzystano interpreter zaimplementowany w Javascript (http://www.skulpt.org/) - a więc uruchamiany bezpośrednio w przeglądare internetowej.
Krótkie wprowadzenie
1) Programy w języku Python składają się z instrukcji wykonywanych po kolei (sekwencyjnie).
Każda instrukcja jest umieszczana w nowym wierszu. Najprostszą instrukcją jest nadanie wartości zmiennym (jeśli zmienna nie istnieje, jest tworzona). Nadanie wartości opisujemy znakiem =. Po lewej stronie umieszcza się identyfikator zmiennej a po prawej wartość. Może to być wyrażenie, liczba lub napis (łańcuch znaków ujęty w cudzysłowy pojedyncze lub podwójne).
Na przykład:
abc = 123
abc – identyfikator zmiennej.
Identyfikatory zmiennych mogą składać się z liter (dużych i małych), cyfr i znaku podkreślenia (_).
2) Poznane wcześniej środowiska programowania (arkusz kalkulacyjny, grafika żółwia) zawierają niejawnie zdefiniowane struktury. Komórki arkusza, czy rysujący żółw są gotowe do użycia bez żadnych działań ze strony użytkownika. W tradycyjnych językach programowania struktury tego typu są zawarte w zmiennych, a podstawową zasadą jest – by te zmienne zainicjować przed użyciem. Poza wartościami (wynikiem wyliczenia wyrażeń arytmetycznych) zmienne mogą zawierać obiekty zdefiniowane przez programistę, lub (częściej) zaimportowane z tak zwanych bibliotek (czyli fragmentów kodu przygotowanych wcześniej i udostępnionych przez twórców). Na przykład jeśli mamy dostępną bibliotekę „turtle” zawierającą definicję działania żółwia, możemy stworzyć obiekt „zolw” i sterować nim poprzez odnoszenie się do tej zmiennej:
import turtle # zaimportowanie biblioteki turtle
zolw = turtle.Turtle() # stworzenie obiektu żółwia
zolw.forward(100) # sterowanie żółwiem
Po znaku # w programie są zawarte komentarze. Nie są one uwzględniane przy wykonaniu programu, ale służą wyjaśnieniu kodu.
Kropka w powyższym przykładzie jest użyta do tego, by przywołać element wewnątrz struktury opisanej przed kropką. Wewnątrz biblioteki turtle jest definicja Turtle z której korzystamy w wierszu drugim. Natomiast utworzony według tej definicji obiekt zolw zawiera metodę poruszania nim: o nazwie forward (wiersz trzeci).
3) Instrukcje mogą tworzyć bloki, wyróżniane spacjami na początku linii. Blok instrukcji oznaczony identyfikatorem nazywa się funkcją. Identyfikator funkcji kończy się nawiasami. W nawiasach tych mogą pojawić się „parametry funkcji”).
Przykład:
def kwadrat(a):
k = a*a
print('kwadrat=%s' % k)
kwadrat(8)
W tym przykładzie identyfikator funkcji kwadrat występuje dwukrotnie. Najpierw (po słowie def) mamy deklarację funkcji (jej opis – nie skutkujący żadnymi działaniami programu).
Potem mamy wywołanie funkcji dla parametru a=8. Wywołanie funkcji jest równoważne przepisaniu w tym miejscu bloku instrukcji funkcji z uwzględnieniem parametrów.
Powyższy program jest więc równoważny do:
a=8
k = a*a
print('kwadrat=%s' % k)
Słowo def jest jednym ze słów kluczowych – czyli słów które twórcy języka zarezerwowali do oznaczenia konstrukcji takich jak pętla (powtórzenia), instrukcja warunkowa, czy (jak wyżej) definicji funkcji. Te słowa nie mogą być użyte jako nazwy zmiennych. Słowa kluczowe pomagają interpreterowi (programowi wykonującemu program w Pythonie) „zrozumieć” (czyli przeanalizować) kod programu.
Definicje nagłówka funkcji, nagłówki instrukcji złożonych itp.. kończą się znakiem dwukropka. Po nim (od nowego wiersza) następuje blok instrukcji.
4) W Pythonie występują oczywiście funkcje warunkowe (if) i pętle. Najczęściej występująca pętla to pętla for.
Przykład:
p=0
n=0
for liczba in [1,2,3,4,5,6,7,8,9]:
if liczba % 2 == 0:
p=p+liczba
else:
n=n+liczba
print('suma parzystych: %s' % p)
print('suma nieparzystych: %s' % n)
Objaśnienie:
W pętli for definiuje się instrukcję lub blok instrukcji wykonywane dla wartości zmiennych opisanych po słowie kluczowym for. W tym wypadku zmienna liczba przyjmuje wartości ze zbioru liczb od 1 do 9 (wyraża to słowo kluczowe in).
Dwa znaki = (==) oznaczają porównanie (jeden – nadanie wartości zmiennej).
Implementacja algorytmów
Sterowanie
Programy standardowo są wykonywane w sposób sekwencyjny - operacja po operacji. Człowiek też nie potrafi myśleć o wielu rzeczach równocześnie. Dlatego tworzone przez niego algorytmy to opis kolejnych operacji, wykonywanych sekwencyjnie (jedna po drugiej). Zakładamy, że komputer będzie odczytywał kolejne instrukcje i zgodnie z nimi zmieniał dane. Przy tym założeniu powstało wiele języków przystosowanych do zapisu algorytmów (zwanych czasem dlatego językami algorytmicznymi).
Pętle
Drugim poza sterowaniem pojęciem, które musimy zrozumieć zanim przejdziemy do algorytmów jest pojęcie pętli. Poznaliśmy je wcześniej jako „powtórzenia” w grafice żółwia. Teraz pora przyjrzeć się im dokładniej.
Zamiast pisać po kolei: 2x2=4, 3x3=9, …. itd., możemy nakazać programowi by dla wszystkich liczb od 1 do 9 wypisał ich kwadraty. Coś w rodzaju:
dla liczb od 1 do 9 drukuj(liczba*liczba)
Oczywiście zapis będzie różny w różnych językach programowania (zazwyczaj pojawi się na początku angielskie słowo ‘for’). Takie wielokrotne wykonywanie zdefiniowanych operacji nazywa się pętlą. Pętla typu for ("dla" - taka jak wyżej) jest obecnie najczęściej stosowana w powiązaniu z przeglądaniem zboru sekwencyjnego (dla liczba w zbiorze [1..9] …..). To nie jest jednak jedyny rodzaj pętli. Wyróżnia się także pętle typu while (dopóki) – czyli wykonywanie tych samych czynności pod pewnymi warunkami (póki istnieją warunki wyrażone przez tak zwany niezmiennik pętli – wyrażenie logiczne) oraz pętla typu repeat (powtarzaj) – czyli wykonywanie operacji tak długo, aż osiągniemy zamierzony efekt – cel wyrażony także przez wyrażenie logiczne. W pętli while warunek sprawdzamy na początku, a wykonanie operacji następuje, gdy jest on prawdziwy (jeśli nie – sterowanie przechodzi do miejsca po pętli). W pętli repeat warunek sprawdza się na końcu, a gdy jest spełniony – nie następuje nawrót do początku. Pętle te są równoważne i czasem występuje tylko pierwsza z nich (while) – która jest bardziej naturalna (to jakby zwielokrotnienie instrukcji warunkowej). To zagadnienie zostanie dokładniej omówione poniżej na konkretnych przykładach.
UWAGA! W języku Python nie ma pętli repeat - ale łatwo ją zastąpić pętlą while. Szczegóły poniżej.
Rysowanie algorytmów
Czasem narysowanie algorytmu w postaci schematu ułatwia jego zrozumienie. Taki schemat jest nazywany schematem blokowym lub schematem przepływu. Pokazuje on jakie wyrażenia są w algorytmie wyliczane, jakie warunki sprawdzane i jak przepływa sterowanie. Na stronie http://www.otwartaedukacja.pl/programowanie/schematy/ dostępne jest oprogramowanie do rysowania takich schematów. Nim narysowano poniższy diagram:
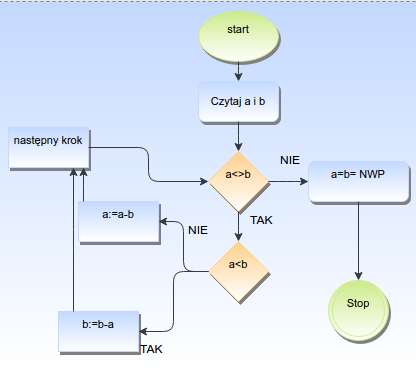
Strzałki pokazują kierunek przepływu, a romby podejmowane decyzje. Znakami := oznaczamy operację podstawienia do zmiennej (a:=9 oznacza, że zmienna a otrzymuje wartość 9). Analizując krok po kroku taki diagram możemy zrozumieć działanie algorytmu.
Diagram przedstawia algorytm Euklidesa (o którym była już mowa). Jest on także przykładem tego, że taki schemat może utrudniać implementację algorytmu zamiast ją ułatwiać. Dlaczego? Rysując schematy powinno się je składać z fragmentów, którym można przyporządkować instrukcje programów. W zasadzie wystarczy trzy rodzaje takicg konstrukcji:
instrukcja warunkowa (wykonanie czegoś jeśli sprawdzony jest warunek);
powtarzanie pod zadanym warunkiem (pętla while);
powtarzanie aż osiągnie się oczekiwany efekt (postawiony warunek – pętla repeat).
Stanie się to jasne, gdy przeanalizujemy przykłady (więcej szczegółów - zobacz kurs Pascala, który opublikował Aleksander Smywiński-Pohl : http://www.apohllo.pl/dydaktyka/wdi/pascal).
Schematy a instrukcje
1. Instrukcja warunkowa (if)
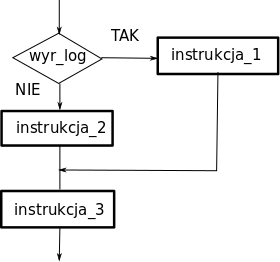
Przykład (Pascal):
if wyr_log then
{instrukcja_1}
else
{instrukcja_2};
{instrukcja_3};
Przykład (Python):
if wyr_log:
# instrukcja_1
else:
# instrukcja_2
#instrukcja_3
2. Powtarzanie pod zadanym warunkiem - pętla while
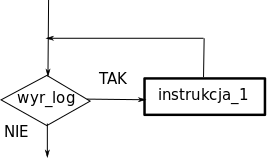
Przykład(Pascal):
var i : integer;
begin
i:=5;
while i>0 do begin
writeln(i);
i:=i-1
end;
end.
Przykład (Python):
i=5
while i>0:
print(i)
i=i-1
- Powtarzanie aż osiągnie się oczekiwany efekt - pętla repeat
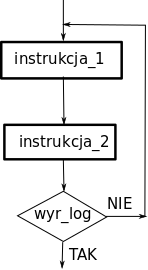
Przykład (Pascal):
var i : integer;
begin
i:=5;
repeat
writeln(i);
i:=i-1
until i=0;
end.
W języku Python nie ma pętli repeat. Można ją zasymulować dzięki istnieniu polecenia break przerywającego pętlę.
Przykład (Python):
i=5
while True:
print(i)
i=i-1
if i==0:
break
Taki sposób programowania nie jest jednak zalecany. Jak widać na tym przykładzie - można zawsze zmieniając warunki przekształcić repeat na while (bez break - zob. opis pętli while).
Od schematu do programu
Wróćmy do narysowanego wcześniej algorytmu NWP aby na tym przykładzie pokazać, jak przekształcić najpierw diagram na postać standardową (złożoną wyłącznie z powyższych wzorców), a następnie na instrukcje.
Schemat algorytmu NWP po przekształceniu na postać standardową:
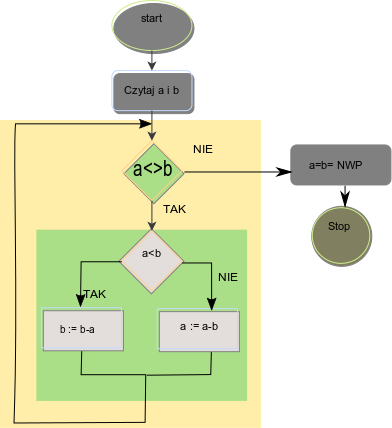
Schemat ten stworzony na portaluhttp://www.otwartaedukacja.pl/programowanie/schematy/
Większe możliwości daje (angielski) portal http://www.js-graph.net/demos/jsgdemoext/.
Poniższy rysunek pokazuje algorytm „rozkomponowany”. Wydzielono dwie „instrukcje”: pętlę powtarzania pod warunkiem (while - zielony) oraz instrukcję warunkową (wykonaj coś pod warunkiem, if, kolor popielaty).
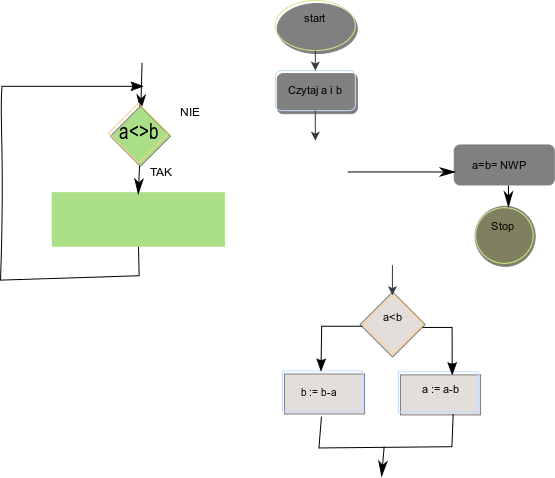
Możemy już zamienić te schematy na instrukcje Pascala. Zastosujemy metodę od ogółu do szczegółu.
Najpierw szkielet programu:
// start
czytaj(a,b);
// szukaj_nwp
wypisz_wynik;
//stop
Teraz sam algorytm:
schemat zielony: while a<>b do [schemat szary]
schemat szary: if a<b then b:=b-a else a:=a-b;
Składamy to wszystko razem:
// start
czytaj(a,b);
// szukaj_nwp
while a<>b do if a<b then b:=b-a else a:=a-b;
wypisz_wynik;
//stop
Na koniec wypełniamy szczegóły
// start
var a,b : integer;
begin
//czytaj(a,b);
write('a=');readln(a);
write('b=');readln(b);
// szukaj_nwp
while a<>b do
if a<b then b:=b-a else a:=a-b;
// wypisz_wynik;
writeln('NWP=',a);
//stop
end.
Ten sam program w Pythonie:
a=input('a=')
b=input('b=')
# szukaj_nwp
while a<>b:
if a<b:
b=b-a
else:
a=a-b
# wypisz_wynik;
print('NWP=%s' %a)
-
Zadania algorytmiczne
Na wstępie podano, że algorytmy to dokładny opis sposobu postępowania prowadzącego do określonego wyniku. Co w tej nieformalnej definicji znaczy „dokładny opis”? Czy każde zadanie można opisać dokładnie? Łatwiejsza jest odpowiedź na to drugie pytanie. Gdy matka prosi córkę: „zaopiekuj się małym braciszkiem”, może dodać szczegółowe przestrogi, ale nie jest w stanie podać wszystkich szczegółów. To nie jest zadanie algorytmiczne – czyli nie istnieje algorytm jego wykonania.
Zadanie algorytmiczne to takie, dla których można podać algorytm rozwiązujący to zadanie. Jeśli ma to być algorytm realizowany przez komputer, to „dokładny opis” obejmuje określenie stanu (zawartości) pamięci. Robimy to posługując się pojęciem danych (zapisanych w pamięci). Można zatem podać dane dla jakich algorytm ma być uruchamiany i oczekiwany wynik w postaci danych wynikowych.
W większości przypadków oczekujemy, że po uzyskaniu konkretnych danych wynikowych algorytm zakończy działanie. Wyjątkiem może być na przykład algorytm sterowania światłami lub wyświetlania aktualnego czasu.
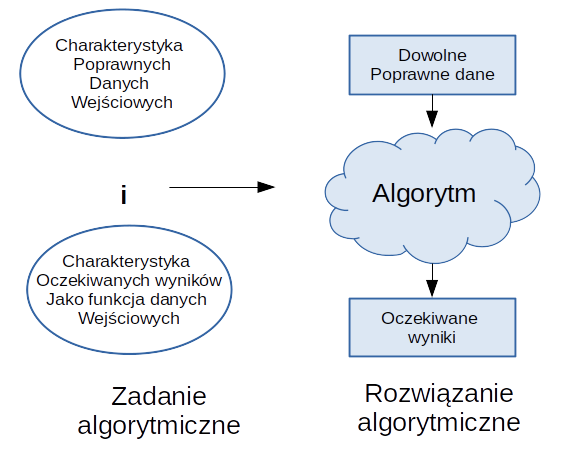
[Rysunek na podstawie: David Harel „Rzecz o istocie informatyki”]
Cechy algorytmów:
- czy zatrzymuje się?
- czy jest poprawny (zwraca prawidłowy wynik dla każdych danych zgodnych ze specyfikacją),
- złożoność obliczeniowa (jak dużo obliczeń wymaga?)
- poziom szczegółowości
Zatrzymajmy się przy tym ostatnim punkcie, gdyż poziom szczegółowości rzadko jest wymieniany wśród cech algorytmów (wynika to stąd, że w przypadku komputerów poziom ten jest zdeterminowany poprzez użyte narzędzia programistyczne).
Wyjaśnimy to na przykładzie z książki „Rzecz o istocie informatyki”1.
Weźmy pod uwagę „pisemne” mnożenie liczb.
Przypuśćmy, ze poproszono nas o pomnożenie liczby 528 przez 46. Wiemy dokładnie, co zrobić. Mnożymy 8 przez 6, otrzymujemy 48, zapisujemy cyfr jednostek wyniku, 8, i zapamiętujemy cyfrę dziesiątek, 4 potem mnożymy 2 przez 6 i dodajemy 4, otrzymujemy 16, zapisujemy cyfrę jednostek, 6, po lewej stronie 8 i zapamiętujemy cyfrę dziesiątek, l itd.
Dlaczego nie możemy rozwiązać całego problemu za jednym pociągnięciem, prostym i zadowalającym algorytmem ,,pomnóż te dwie liczby"? Dlaczego wolno nam bezpośrednio pomnożyć 6 przez 8, ale nie 528 przez 46? Z drugiej strony – skąd wiemy ile to jest 8 razy 6? Dlaczego algorytm nie zawiera polecenia by sprawdzić to w „tabliczce mnożenia”?
To są pytania o poziom szczegółowości.
Poziom szczegółowości to krytyczna cecha decydująca o tym, czy zaakceptujemy algorytm mnożenia. Przyjmujemy, ze stosowny sprzęt (w tym przypadku my sami) jest zdolny wykonać ,,8 razy 6", ale nie ,,528 razy 46", i że możemy to zrobić w naszych głowach albo przynajmniej znamy jakiś inny sposób, więc nikt nie musi nam mówić, jak wyszukiwać wynik w tabliczce.
Gdy stosowany sprzęt potrafi mnożyć dowolne liczby (komputer) – zadanie staje się trywialne. Chyba że chodzi o szybkie pomnożenie bardzo dużych liczb ….
Algorytmika
Poza zadaniami których rozwiązanie tkwi w samym opisie (pozostaje jedynie przełożyć ten opis na język programowania), układanie algorytmów nie jest zadaniem algorytmicznym!!! Nad niektórymi algorytmami twórcy głowią się miesiącami (nawet latami). Nie można określić z góry ile nam to czasu zajmie.
Przykład:
Szeryf ma w areszcie trzech skazańców. Nie kontaktują się oni ze sobą ani się nie widzą. Szeryf – amator gotowania, wymyśla pewnego dnia zabawę. Od następnego dnia będzie zapraszał każdego dnia jednego z więźniów na ucztę. Potem wszyscy głosują: tak lub nie w odpowiedzi na pytanie: czy wszyscy jedli co najmniej raz. Jeśli co najmniej dwóch zagłosuje poprawnie „tak” - gdy rzeczywiście wszyscy jedli – wychodzą na wolność. Jeśli wszyscy trzej zagłosują na „tak” i się pomylą – wyrok śmierci zostanie wykonany. Więźniowie mają wspólnie ustalić algorytm postępowania.
Ta zagadka logiczna przy powyższych założeniach ma proste rozwiązanie, ale wcale nie wynika ono z opisu i nie każdy będzie miał cierpliwość by je znaleźć. Aby znaleźć to rozwiązanie należy bowiem porzucić myślenie o przekazywaniu informacji kto już jadł, a pomyśleć o zabezpieczeniu przed błędnym głosowaniem. Wystarczy by ten, który je pierwszego dnia nie głosował nigdy, a pozostali wtedy, gdy już byli na uczcie. Co jednak mają więźniowie zrobić, gdy nie określono od kiedy zaczną się uczty, a na dodatek mają zgadnąć w najbliższym możliwym terminie (rozwiązanie poniżej2)?
Takie zagadki są interesujące i mogą urozmaicać lekcje, ale traktowanie ich jako typowych zadań może jedynie utrwalać przekonanie, że programowanie jest sztuką trudną.
Nie można zatem oczekiwać, że na lekcjach w szkole uczniowie będą wymyślać algorytmy-poza przypadkami, gdy te algorytmy tkwią w samym opisie zadania i pozostaje jedynie przełożyć je na język programowania.Można i należy jednak uczyć układania prostych algorytmów oraz rozumienia bardziej złożonych algorytmów wymyślonych przez „algorytmików”.
Przykład zadanie którego rozwiązanie tkwi w opisie podaje Krzysztof Diks (UW) podczas interesującego wykładu „Po co komu te algorytmy?” (od minuty 16:00). https://www.youtube.com/watch?v=Xmudle0HjWk. Jest to przykład z matury w roku 2005 (https://www.cke.edu.pl/images/stories/Matura2005/inf_a2.pdf – zadanie 5).
Najlepszą sumą ciągu liczb a1, a2, .., an nazywamy największą wartość wśród sum złożonych z sąsiednich elementów tego ciągu. Na przykład dla ciągu: 1, 2, –5, 7 mamy następujące sumy:
1, 1+2 = 3, 1+2+(–5) = –2, 1+2+(–5)+7 = 5, 2, 2+(–5) = –3, 2+(–5)+7 = 4, –5, –5+7 = 2, 7.
Zatem najlepszą sumą jest 7 (zwróć uwagę, że jeden element też uznajemy za sumę).
Przełożenie warunków tego zadania na język Python:
# lista = lista liczb całkowitych, na przykład
lista=[1, 2, –5, 7]
# wylicz sumę każdej podlisty (fragmentu listy) lista[start:gora]
# start – indeks pierwszego elementu podlisty
# gora – indeks pierwszego elementu poza podlistą
# zwróć największą z sum
Powyższy zapis jest chyba zupełnie jasny i oczywisty. Objaśnienia wymaga jedynie konstrukcja lista[a:b]. W Pythonie tak zapisuje się fragmenty listy. Indeksy liczymy od 0. Zatem fragment lista[1:3] dla powyższego przykładu to [2,-5] (element o indeksie 3 – czyli liczba 7 nie wchodzi już do fragmentu listy).
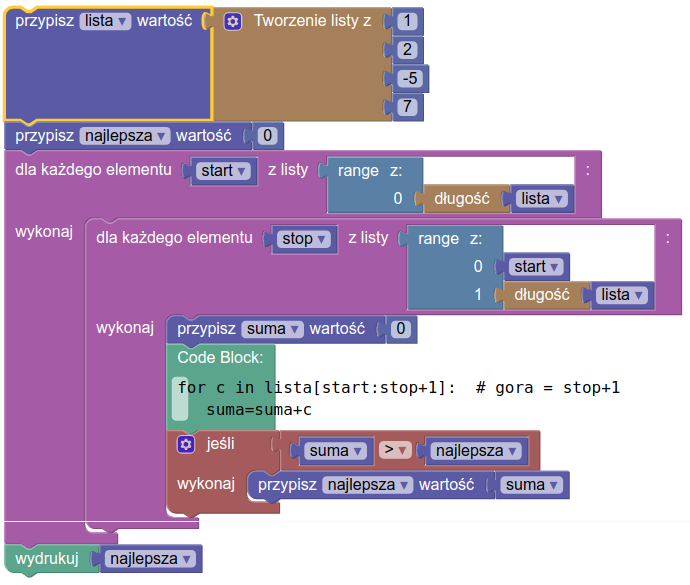
Rozwiązanie jest trywialne:
lista=[1,2,-5,7]
najlepsza=0
for start in range(len(lista)):
for stop in range(start,len(lista)):
suma=0
for c in lista[start:stop+1]: # gora = stop+1
suma=suma+c
if suma>najlepsza:
najlepsza=suma
print('Najlepsza=%s' % najlepsza)
Objaśnienia wymagają jedynie dwie użyte funkcje:
len – zwraca długość listy (ilość elementów)
range – zwraca po kolei liczby całkowite z podanego zakresu.
Gdy podano jeden parametr – funkcja range zwraca liczby począwszy od zera (0). Gdy dwa parametry – pierwszy określa od jakiej liczby startujemy. W obu przypadkach zwracane są liczby nie większe od ostatniego podanego parametru.
Na przykład range(3) zwróci 0,1,2 natomiast range(1,3) zwróci 1,2.
Powyższy algorytm można zapisać w postaci bloczków, ale ten zapis nie będzie wcale bardziej czytelny (jak widać poniżej jedna z pętli została przytoczona w postaci kodu):
Od maturzystów wymagano, aby dla powyższego zadania znaleźć bardziej optymalny algorytm, co jest chyba nieporozumieniem. Jeśli ktoś zaliczył ten egzamin – może spokojnie pójść do pracy jako programista. Efekt – średnia zdawalność poniżej 30% (w przygotowaniu matury były też inne błędy3).
Dla porządku przytoczmy optymalne rozwiązanie:
lista=[1,-2,2,2,-5,3,3,1,-3]
najlepsza = 0
rnajlepsza = 0 # potencjalnie najlepsza zawierająca ostatni element
for liczba in lista:
rnajlepsza+=liczba
if rnajlepsza<liczba:
rnajlepsza=liczba
if rnajlepsza>najlepsza:
najlepsza=rnajlepsza
print(najlepsza)
Przypisy:
1David Harel „Rzecz o istocie informatyki”
2Głosują na tak wszyscy którzy już jedli, poza tym - który jadł w dniu głosowania.