Matematyka i programowanie
Kiedyś na komputery mówiono „maszyny matematyczne”, a ich działanie nazywano obliczaniem. Co wspólnego z matematyką ma na przykład pisanie tekstu na komputerze? Każda informacja w komputerze może być traktowana jak ciąg liczb. Dlatego informatyka i matematyka są nierozerwalnie ze sobą związane. Wyodrębniono nawet dziedzinę matematyki zwaną matematyką dyskretną, która ma zastosowanie w informatyce. W tym podręczniku przedstawimy tylko wybrane elementy matematyki dyskretnej, które mają szczególne znaczenie dla programisty.
Warto w tym miejscu zauważyć, że matematyka jest także ulubionym źródłem zadań algorytmicznych (także na maturze: https://www.p-programowanie.pl/dzial/matura-z-informatyki/). Nie znaczy to wcale, że programista musi być dobrym matematykiem. W obu wypdakach wymagana jest umiejętność abstrakcyjnego i logicznego myślenia. Ale większość matematycznych problemów z jakimi się styka programista zostało już rozwiązane i można skorzystać z gotowych implementacji (bibliotek).
Algebra Boole’a
Logika w programach komputerowych pełni bardzo ważną rolę. Instrukcje warunkowe i pętle zawierają warunki, które są sprawdzane w czasie wykonywania programu. Algebra Boole’a pozwala na traktowanie wartości logicznych podobnie jak liczb. Czyli możemy wartość warunku wyliczyć i zapisać w zmiennych. Możemy też posługiwać się operatorami logicznymi (lub/i/nie) tak jak arytmetycznymi – stosując nawiasy, wykorzystując hierarchię ważności operatorów, łączność i rozdzielność.
Przykład:
a=read('a=')
b=read('b=')
while a != b:
doma = a>b
if doma:
a:=a-b
else:
b:=b-a
print('NWP=',a)
Zmienna doma w tym przykładzie ma wartość logiczną: jeśli a>b to doma przyjmuje wartość PRAWDA. W przeciwny przypadku będzie ona miała wartość FAŁSZ. Wszędzie tam, gdzie trzeba podać warunek, można wpisać identyfikator zmiennej. Jest to równoważne z warunkiem doma = PRAWDA (w języku Python: doma==True).
Znaczenie teoretyczne
Algebra Boole’a pozwana na uzasadnienie tezy, że komputer to „maszyna logiczna” (wylicza wartość wyrażeń logicznych).
Pamięć komputera zawiera bity. Co to dokładnie znaczy? Bit to najmniejsza porcja informacji – wybór jednego z dwóch elementów. Najczęściej wybieramy między zerem a jedynką (tak jest w komputerach). Odpowiada to oczywiście wartościom fałsz (zero) i prawda (jeden) w logice. Sposób ich zmiany jest na poziomie sprzętu zdeterminowany połączeniami zwanymi bramkami logicznymi.
Zaprojektujmy sobie najprostszy komputer, który komputer, który liczy jedynie sumy wyłączne (XOR) z sygnałów podanych na wejściu. Suma wyłączna (A XOR B) czyli inaczej „albo albo” daje na wynik prawdę, gdy prawda jest na wejściu A albo na wyjściu B, ale nie na obu. Natomiast iloczyn (A i B, A AND B) daje prawdę, gdy zarówno A jak i B mają wartość prawda.
Odpowiedni przykład funkcji przejścia można przetestować na stronie http://logic.ly/demo/ (trzeba wybrać przykład opisany jako „1-Bit Full Adder”):
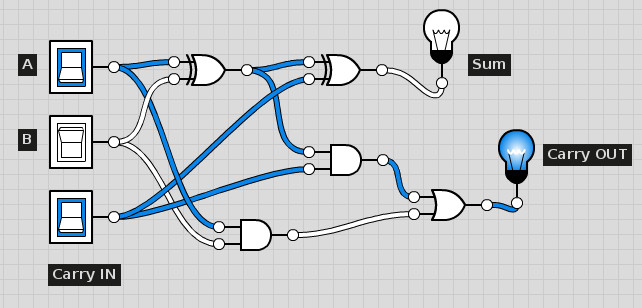
Zmieniając przyciski A i B możemy obserwować co dzieje się na wyjściu – czy pali się lampka Sum. W tym przykładzie mamy dodatkowo sygnały przeniesienia (Carry IN na wejściu i Carry OUT na wyjściu). Umożliwiają one połączenie kaskadowo tych sumatorów dla uzyskania sumy z więcej niż dwóch wejść (wynik Carry OUT łączymy do Carry IN z następnej pary).
Żeby można było mówić o komputerze, a nie tylko o układzie elektronicznym, poszczególnym elementom wejścia i wyjścia muszą odpowiadać komórki pamięci, a wynik obliczeń powinien zostać zapisany w komórkach odpowiadających wyjściu w takt zegara odliczającego instrukcje.
W tak prostym przykładzie mamy 5 jednobitowych komórek pamięci i 5 układów elektronicznych (bramek logicznych).
Jaka zatem powinna być złożoność komputera przetwarzającego informację o złożoności liczonej w milionach bitów? Ogromna. Prostszym jest pytanie postawione od drugiej strony: ile maksymalnie bitów zmieniają za jednym razem współczesne komputery? Jeśli słyszymy, że mamy procesor 64-bitowy, to oznacza właśnie tyle, że naraz może odczytać lub zapisać 64 bity. Większą ilość komórek pamięci można zmienić w wielu kolejnych taktach zegara. Niektóre obliczenia są tak złożone, że takie sekwencyjne (krok po kroku) obliczenia nie skończyłyby się nawet za tysiąc lat.
Czy komputery są bezbłędne?
Skoro logika determinuje działanie komputera, to jak jest możliwe to, że może on „robić błędy”? To wina użytkownika lub programisty. Weźmy na przykład fragment programu:
jeśli a>=b to napisz(‘a>b’);
jeśli a<=b to napisz(‘a<b’);
Program dla a=b napisze, że a>b i a<b równocześnie. Takie błędy (użycie złego znaku porównania) są bardzo często spotykane. Jak to ma się do tezy, że w komputerze nie może być sprzeczności? Na poziomie kodu maszynowego nie ma żadnej sprzeczności w działaniu. Komputer wypisuje w określonej sytuacji określony wynik on nawet „nie wie”, że drukowany napis ‘a>b’ zawiera wyrażenie logiczne (dla niego to tylko dana – ciąg bitów).
Logiczne myślenie – uwaga metodologiczna:
Wyrażenia logiczne mogą być bardzo złożone. Dlatego logikę – czyli najbardziej naturalną umiejętność człowieka postrzegamy dzisiaj jako rzecz trudną. Nauki logiki nie powinno się zaczynać od operowania na symbolach i wyrażeniach, ale od prostych pytań w rodzaju: co zrobić, aby osiągnąć jakiś efekt. To mogą być proste historie (na przykład: aby włączyć notebooka trzeba podnieść klapę i nacisnąć przycisk, ale jeśli bateria jest rozładowana, musimy włączyć go dodatkowo do prądu). Po dojściu do końca w analizie postawionego problemu, można zapisać działania w odpowiedniej kolejności, uzyskując prosty algorytm.
Kombinatoryka i złożoność obliczeniowa
Kombinatoryka zajmuje się badaniem liczności zbiorów konstruowanych w różny sposób (na przykład przez kombinacje, permutacje). Tymczasem komputer może nie tylko łatwo policzyć, ale skonstruować każdy zbiór. Służą do tego pętle.
Na przykład lista uporządkowanych par liczb nie powtarzających się:
lista=[]
max=input('najwieksza liczba=')
for a in range(1,max+1):
for b in range(1,max+1):
lista.append((a,b))
print('ilosc=%s' % len(lista))
Program generuje zbiór par liczb naturalnych. A więc kombinacje (http://www.math.edu.pl/kombinacje) dwuelementowe.
W ten sam sposób można dla każdego kombinatorycznego zagadnienia stworzyć program wykonujący konstruowanie odpowiednich zbiorów. Częściej jednak mamy do czynienia z zagadnieniem odwrotnym: mamy program przeglądający lub konstruujący zbiory, a kombinatoryka służy do ustalenia złożoności tych obliczeń
Zobacz też: http://pl.numberempire.com/combinatorialcalculator.php
Arytmetyka w komputerach
Prędzej czy później w każdym kursie informatyki pada stwierdzenie: komputer liczy w systemie dwójkowym. Teraz nastąpił ten moment ;-). Tak liczy w systemie dwójkowym – i co z tego? Dlaczego programistę może / powinno to interesować?
Najważniejszym powodem jest to, że można obliczyć jakie największe liczby mogą być zapamiętane w zmiennej. Dla przykładu gdyby zmienna miała 8 bitów (bajt) – to oznacza, że pamięta liczby o ośmiu cyfrach. Ponieważ zaś mamy do czynienia z systemem dwójkowym – są to cyfry 0 lub 1.
Największa możliwa do zapamiętania liczba to oczywiście liczba 11111111 zapisana dwójkowo (czyli 255). To wcale nie jest dużo. Dlatego zazwyczaj przyjmuje się do pamiętania liczb zmienne o większej wielkości (minimum dwa bajty). To nadal w różnych obliczeniach może być mało (dwa bajty to tylko 255*255). Jeśli dopuszczamy liczby ujemne – to dodatkowo odpada nam jeden bit na zapamiętanie znaku. Dla naprawdę dużych liczb konieczne są inne sposoby ich pamiętania i specjalne sposoby liczenia. Nie będziemy się w to wgłębiać, ale powinniśmy wiedzieć – że występują w komputerach tego typu problemy i dlatego wprowadzono „liczby zmiennoprzecinkowe”.
Najlepiej wyjaśnić to na przykładzie. W konsoli języka PHP (uruchomienie php -a) możemy napisać:ista
php -a
php > $a = 2;
php > $b = 2.0;
php > if ($a==$b) print 'jednakowe';
jednakowe
php > if ($a===$b) print 'jednakowe';
php > if ($a===(int)$b) print 'jednakowe';
jednakowe
php >
Objaśnienie:
Liczby całkowite są innego typu niż rzeczywiste (w komputerze nazywane „zmiennoprzecinkowymi). Podwójne znaki równości (==) oznacza porównanie wartości zmiennych z niejawną konwersją typów. Dlatego liczba rzeczywista i całkowita są równe.
Potrójny znak = (===) oznacza warunek, by równość była dokładna. Czyli 2.0 to nie to samo co 2. Możemy zastosować konwersję jawną (int)$zmienna oznacza taką konwersję do liczby całkowitej (bierze całkowitą część liczby).
W języku Pascal jawnie deklarujemy typy zmiennych. Pokażemy to na przykładzie algorytmu Leibniza wyliczania liczby pi:
var mianownik, dokladnosc, pi4,poprzedni,znak : real;
begin
mianownik:=1;
dokladnosc:=0.0001;
pi4:=1;
poprzedni:=0;
znak:=-1;
while abs(pi4-poprzedni)>dokladnosc do begin
mianownik:=mianownik+2;
poprzedni:=pi4;
pi4:=pi4+znak*(1/mianownik);
znak:=-znak;
end;
writeln(pi4*4:7:5)
end.
Typ real to liczby zmiennoprzecinkowe (liczby całkowite to integer).
W języku Python (wersja 2.x) zmienna jest inicjowana poprzez podstawienie. Dlatego musimy zapisać odpowiednio stałe (jeśli zamiast 1.0 wpiszemy do mianownika 1 - algorytm nie zadziała).
mianownik=1.0
dokladnosc=0.0001
pi4=1.0
poprzedni=0.0
znak=-1
while abs(pi4-poprzedni)>dokladnosc:
mianownik=mianownik+2.0
poprzedni=pi4
pi4=pi4+znak*(1/mianownik)
znak=-znak
print('pi=%s' % (pi4*4))
Matematyka i informatyka w edukacji
Małe dzieci mają się obecnie uczyć dwóch tak zwanych „przedmiotów ścisłych”: matematyki i informatyki. Są one ściśle ze sobą powiązane, choć matematyk zapewne wolałby powiedzieć – że to informatyka jest dziedziną zależną od matematyki (a nie odwrotnie). Czy zatem nauczanie matematyki nie powinno poprzedzać nauczania informatyki? Odpowiedź na to pytanie nie jest oczywista. W szczycącej się najlepszym systemem edukacji Finlandii trwa reforma mająca na celu rezygnację ze ścisłego podziału na przedmioty (http://www.juniorowo.pl/nauka-w-szkole-bez-podzialu-na-przedmioty/). Zamiast tego dzieci mają w małych zespołach pracować nad rozwiązywaniem problemów i tworzeniem projektów. Z całym szacunkiem dla matematyki, należy stwierdzić że w takim procesie nauczania informatyka ma znacznie więcej do zaoferowania. Nie chodzi tylko o rozwijane we współpracy z producentami gier komputerowych nauczanie przez zabawę. Ważniejsze jest to, że informatyka (a programowanie w szczególności) rozwija się właśnie dzięki współpracy osób o różnych zakresach kompetencji. Aby tą współpracę ułatwić, stosuje się zasadę: proste jest lepsze niż skomplikowane. Także jednym ze wskaźników jakości produktów informatycznych jest prostota (łatwość stosowania). Tymczasem matematyka w pogoni za ścisłością wydaje się być skazana na narastający (wraz z jej zgłębianiem) poziom komplikacji. Bez opanowania arytmetyki nie możemy rozwiązywać równań, a bez nich nie ma mowy o układach równań etc… Matematyczne wywody mogą być upraszczane przez użycie wcześniej udowodnionych twierdzeń, podobnie jak programista upraszcza sobie życie korzystając z gotowych modułów. Jednak podejście programisty jest bardziej pragmatyczne. Pisząc moduły kładzie nacisk na wyjaśnienie jak ich użyć. Matematyk opisując twierdzenie stara się je wyjaśnić lub udowodnić.
Załóżmy, że programista który nic nie wie o geometrii ma za zadanie obliczyć pole zakreślone przez okrąg o promieniu 4. Chwila szperania w internecie pozwala znaleźć bibliotekę SymPy. Na podstawie przykładów buduje prosty skrypt (po znaku # komentarze):
from sympy.geometry import Circle,Point
okrag=Circle(Point(0,0),4) # okrąg w punkcie o współrzędnych 0,0
print("pole=%s" % okrag.area)
print("liczbowo: %s" % float(okrag.area)) # float = liczba rzeczywista
# program drukuje:
# pole=16*pi
# liczbowo: 50.2654824574
Na lekcji informatyki uczeń tak rozwiązujący zadanie dostanie piątkę – nawet jeśli nie wie jaki jest wzór na pole okręgu. Na lekcji matematyki brak tej wiedzy może skutkować dwóją.
Czy zatem informatyzacja matematyki prowadziłaby do produkcji tumanów potrafiących korzystać z gotowców bez zrozumienia?
Nie. Zarówno świat matematyki jak i informatyki to cudowny świat abstrakcji, którego zgłębianie może sprawiać wiele radości. Pragmatyczne podejście programisty jest przy tym dużym ułatwieniem. Jednak matematyka nie tylko zaspokaja ciekawość (jak to jest zrobione) ale pozwala na doskonalenie tworzonych rozwiązań [zob opinię programisty]. Ta ciekawość i chęć doskonalenia powinny być rozbudzane wśród dzieci. Prymat pragmatycznej informatyki nad matematyką może to bardzo ułatwić.
Weźmy inny prosty przykład: zsumowania wszystkich liczb jednocyfrowych:
liczby=[0,1,2,3,4,5,6,7,8,9]
suma=0
for liczba in liczby:
suma=suma+liczba
print('suma=%s' % suma)
Jednak matematyka pozwala nam spostrzec, że te liczby tworzą ciąg arytmetyczny którego sumę wyliczamy jako połowę sumy pierwszego i ostatniego elementu pomnożonej przez ilość elementów. Czyli nasz program uległ drastycznemu uproszczeniu:
suma=(0+9)*10/2
print('suma=%s' % suma )
Typy danych jako struktury abstrakcyjnego świata
W abstrakcyjnym świecie opisywanym przez programistę występują dane (wartości przyjmowane przez zmienne) różnych typów i tworzące różne struktury. Przykładami typów danych są liczby wymierne (float) lub całkowite (int). Szersze wyjaśnienie znajdziemy na stronie „Ważniaka” (http://wazniak.mimuw.edu.pl – naprawdę warta polecenia każdemu pasjonatowi informatyki).
W najprostszym ujęciu typ to pewien ustalony zbiór wartości (w domyśle: które mogą być przyjmowane przez zmienne). W praktyce z każdym typem związany jest zbiór operacji, które można wykonywać na wartościach z tego typu. Tak postawiona definicja bliska jest klasycznemu pojęciu zbioru — z konieczności skończonego, gdyż pamięć mamy skończoną.. [Paradygmaty_programowania]
Jeśli definiujemy zbiór danych wraz z operacjami na nich wykonywanymi, to mamy do czynienia z obiektami (w informatyce) lub strukturami algebraicznymi (w matematyce). Jedną z najprostszych struktur algebraicznych jest grupa. Jest to para (zbiór, działanie), która spełnia następujące warunki (w przykładach działanie oznaczam znakiem #):
- działanie jest łączne - czyli (a#b)#c = a#(b#c),
- działanie posiada wyróżniony element neutralny (oznaczmy 0) - czyli taki, że dla dowolnego x: x#0=x,
- każdy element posiada element odwrotny – czyli jeśli e’ jest odwrotnością do e to e’#e=0
Taką grupą będzie na przykład zbiór liczb całkowitych z operacją dodawania.
Aby pokazać zasadność definiowania takich abstrakcyjnych struktur przytoczmy przykład liczb mniejszych niż 100. Możemy je traktować jako reszty z dzielenia przez 100.
Możemy zdefiniować działanie dodawania summ:
- jeśli a+b >=100 to summ(a,b) = a+b-100
- jeśli a+b <100 to summ(a,b) = a+b
W powyższym opisie stosujemy konwencję funkcyjnego zapisu działania. Zamiast summ(a,b) możemy równie dobrze zapisywać a#b (traktując ten opis jako definiowanie #).
W języku Python możemy zdefiniować taką strukturę jako klasę obiektów:
class Modulo100:
neutralny = 0
def dzialanie(self,a,b):
if a+b>100:
return a+b-100
else:
return a+b
def odwrotny(self,a):
return 100-a
A oto przykład użycia:
liczby = [1,4,7,77,98]
suma=0
grupa=Modulo100()
for liczba in liczby:
suma=grupa.dzialanie(suma,liczba)
print('suma=%s' % suma)
Przechodząc na wyższy poziom abstrakcji możemy stworzyć klasę reprezentującą typ danych (a nie klasę zawierającą operacje na typie danych jak wyżej):
#!/usr/bin/env python3
class Modulo100:
def __init__(self, liczba):
self.liczba = liczba
@classmethod
def neutralny(cls):
return Modulo100(0)
def dodaj(self, skladnik):
if self.liczba + skladnik.liczba >= 100:
return Modulo100(self.liczba + skladnik.liczba - 100)
else:
return Modulo100(self.liczba + skladnik.liczba)
def odwrotny(self):
if self.liczba == 0:
return self
else:
return Modulo100(100 - self.liczba)
if __name__ == "__main__":
liczby = [Modulo100(1), Modulo100(4), Modulo100(7), Modulo100(77), Modulo100(98)]
suma = Modulo100.neutralny()
for liczba in liczby:
suma = suma.dodaj(liczba)
print('suma=%s' % suma.liczba)
Powyższy przykład pokazuje, że użycie klas i obiektów do opisu abstrakcyjnych struktur ma walor praktyczny. Ten sam sposób opisu można stosować do różnych rodzajów działań. Tworzyć można też bardziej złożone struktury (zob abstrakcyjne typy danych, ang. abstract data type) – takie jak stos (LIFO, stack), kolejka (FIFO, queue), czy graf (graph).
Relacyjne bazy danych
Większość zbiorów danych przetwarzanych komputerowo ma bardzo prostą strukturę – choć są bardzo liczne (mają wiele elementów). Informacje w komputerze dotyczące elementów tych zbiorów sprowadzają się do powiązania ich z cechami / atrybutami. Na przykład zbiór gwoździ na magazynie dzieli się jedynie według wielkości. Nie rozróżniamy poszczególnych sztuk takiej samej wielkości. Z kolei osoby ze zbioru pracowników muszą być rozróżniane – nawet jeśli mają takie samo nazwisko. Dlatego często wprowadza się jednoznaczny numer kadrowy.
Teoretycznie można zbudować funkcję, która zwraca (wylicza) atrybuty (cechy) każdego elementu zbioru. Na przykład pensję zasadniczą każdego pracownika może zwracać funkcja: płaca_zasadnicza(pracownik)
Co jednak ma być parametrem takiej funkcji (co oznacza identyfikator „pracownik”)? Przecież nie osoba fizyczna. Nazwisko? A może PESEL? Albo wspomniany numer kadrowy (bo przecież obcokrajowcy nie mają numerów PESEL)?
Innym problem pojawia się wraz z pytaniem: jakie jeszcze funkcje (poza tą zwracającą wynagrodzenie) będą nam potrzebne? Czy jesteśmy w stanie wszystkie przewidzieć? Czy programista musi je zdefiniować?
Rozwiązanie tych dylematów okazuje się stosunkowo proste, jeśli zamiast funkcjami będziemy operować ich uogólnieniem – relacjami.
Weźmy na przykład funkcję zwracającą numer pracownika o zarobkach mniejszych niż zmieniona płaca minimalna (musimy im podwyższyć): pracownik_o_zarobkach(kwota)
Funkcja zwraca nam dla każdej unikalnej wartości parametr dokładni jedną wartość. Ale przecież pracowników takich może być wielu. Możemy przyjąć, że wynikiem funkcji jest zbiór danych (nie narysujemy wykresu takiej funkcji, ale to nadal będzie funkcja). Możemy jednak zamiast tego operować pojęciem relacji. Zanim dokładnie je wyjaśnimy, możemy przyjąć, że są to dane w postaci tabeli (takiej jak w arkuszu kalkulacyjnym).
Na przykład:
| Numer | Pesel | Nazwisko | Pensja | ….. |
|---|---|---|---|---|
| 101 | ….. | Jan Nowak | 1800 | |
| 102 | … | Jan Kowalski | 2100 | |
| 103 | … | Marek Malinowski | 1750 |
Chcąc wybrać numery i pensje pracowników zarabiających poniżej 2000 otrzymamy:
| Numer | Pensja |
|---|---|
| 101 | 1800 |
| 103 | 1750 |
W żadnym takim zestawieniu nie istnieje byt elementarny (zmienna, prosta wartość), który reprezentuje pracownika. Pracownik to tylko zbiór atrybutów (cech). Na przykład (101, Jan Nowak, 1800, ……). Czyli mamy połączenie zbiorów różnych wartości (numery, nazwiska, pensje etc….).
Takie połączenie nazywa się w matematyce iloczynem kartezjańskim zbiorów. Natomiast tabelki takie jak wyżej to podzbiór iloczynu kartezjańskiego zbiorów – nazywany relacją.
Zilustrujmy różnicę prostym przykładem:
- zbiór_numerów = (101,102,103)
- nazwiska = (Jan Kowalski, Jan Nowak, Marek Malinowski)
- iloczyn kartezjański zbiór_numerów x nazwiska = [(101,Jan Kowalski),(101, Jan Nowak),(101, Marek Malinowski),(102,Jan Kowalski),(102, Jan Nowak),(102, Marek Malinowski),(103,Jan Kowalski),(103, Jan Nowak),(103, Marek Malinowski)]
- relacja = [(102,Jan Kowalski),(101, Jan Nowak),(103, Marek Malinowski)]
Czyli relacja zawiera te pary z iloczynu kartezjańskiego, które zawierają realną informację.
Zamiast par elementem iloczynu kartezjańskiego mogą być trójki, czwórki itd… Określamy je ogólnie terminem „krotka”. Mówimy zatem, że relacje to zbiory krotek (odpowiadają one wierszom tabeli nazywanym czasem rekordami).
Możemy zatem zdefiniować iloczyn kartezjański zbiorów D1, D2, ... , Dn jako zbiór wszystkich krotek (x1,x2, ... , xn) takich, że x1 jest elementem zbioru D1, x2 jest elementem zbioru D2, ... , xn jest elementem zbioru Dn. Natomiast podzbiór iloczynu kartezjańskiego nazywa się relacją.
Każdy element krotki nazywamy atrybutem (w naszym przykładzie relacja zawiera krotki składające się z dwóch atrybutów: numeru i nazwiska).
Z każdej relacji możemy wybrać (wyselekcjonować) krotki o określonych wartościach atrybutów. Na przykład atrybut numer równy 101 ma tylko jedna krotka (101, Jan Nowak). Jeśli możemy wskazać atrybuty, które dla każdej możliwej wartości wskazują na co najwyżej jedną krotkę (jednoznacznie identyfikują krotki), to taki zbiór atrybutów nazywa się kluczem głównym relacji (w naszym przykładzie atrybut numer jest kluczem głównym).
Relacjom często nadaje się nazwy.
Nazwa relacji wraz z określeniem zbioru cech (atrybutów) z których relacja powstała nazywa się schematem relacji. Na przykład schemat relacji opisującej pracowników może wyglądać następująco:
PRACOWNICY(NUMER, NAZWISKO,PESEL, PENSJA).
Powyższe rozważania mają charakter teoretyczny, ale odnoszą się do jednego z podstawowych rozwiązań stosowanych w programowaniu: baz danych. Bazy danych to mechanizmy pamiętania danych opisywanych relacjami oraz mechanizmy selekcji (wyboru) tych danych.
Do zapamiętywania danych służą tabele (odpowiedniki relacji), a selekcji wykonujemy przy pomocy zapytań formułowanych w języku SQL. Język zapytań SQL jest stosunkowo prosty i warto przyswoić sobie jego podstawy.
Podstawowa składnia takiego zapytania:
SELECT atrybuty FROM relacje WHERE warunki
Słowa kluczowe oznaczają:
- SELECT – wybór
- FROM – (z) – z jakich relacji
- WHERE – dla jakich warunków selekcji
Na przykład:
SELECT numer, pensja FROM pracownicy WHERE pensja<2000;
W miejscu relacji mogą pojawiać się identyfikatory tabel lub podzapytania reprezentujące tabelę wynikową (zobaczymy to w dalszych przykładach).
Algebra relacji
Dzięki temu, że podstawą baz danych jest ścisła teoria matematyczna, możemy dokonać analizy w celu wypracowania metod optymalnej organizacji struktur danych (schematów bazy danych) oraz metod ich przetwarzania.
Poniżej opisano podstawowe operacje na relacjach rozważane w tej teorii:
- Suma i różnca
Suma relacji A i B jest zbiorem wszystkich krotek należących do relacji A lub należących do relacji B i tylko takich. Na przykład zbiór (relacja) pracowników może być sumą zbioru pracowników o fizycznych i umysłowych. Albo takich którzy mają zbyt małą pensję i pozostałych.
Możemy zapisać w SQL:
SELECT * FROM pracownicy A WHERE A.pensja<2000;
SELECT * FROM pracownicy B WHERE B.pensja>=2000;
Gwiazdka oznacza wszystkie atrybuty. Identyfikator po określeniu tabeli (A, B) oznacza nazwę (pseudonim, alias), jaki nadajemy tabeli w tym zapytaniu. Kropka rozdziela nazwę tabeli i atrybut (A.pensja to atrybut pensja w relacji/tabeli A). Stosowanie aliasów jest ważne zwłaszcza w bardziej złożonych zapytaniach – składających się z wielu tabel.
Rożnica relacji A i B jest zbiorem tych krotek relacji A, które nie należna do relacji B i tylko takich. Jeśli na przykład mamy relację B – pracowników których pensja wynosi co najmniej 2000, to możemy zdefiniować różnicę między zbiorem wszystkich pracowników i tabelą B.
Różnicę można zdefiniować w SQL korzystając operatorów IN (istnieje w zbiorze) lub NOT IN (nie istnieje w zbiorze). Czyli SELECT * FROM pracownicy p WHERE p.numer NOT IN <numery_z_B>.
Zbiór numerów to oczywiście:
SELECT B.numer FROM pracownicy B WHERE B.pensja>=2000;
W języku SQL zasadniczo całość zapytania musi być zapisana łącznie (bez definiowania numery_z_B gdzie indziej). Czyli cały poprawny zapis wygląda następująco:
SELECT * FROM pracownicy p WHERE p.numer NOT IN (SELECT B.numer FROM pracownicy B WHERE B.pensja>=2000)
Iloczyn kartezjański
Iloczyn kartezjański relacji A o krotności k1 oraz B o krotności k2 jest zbiorem (k1+k2)-krotek, których pierwsze k1 składowych jest k1-krotką pochodzącą z A, a ostatnie k2 składowych jest k2-krotka pochodząca z B.
Na przykład iloczyn kartezjański podzbioru pracowników (numer, nazwisko) i etatów:
SELECT * from
(SELECT numer, nazwisko FROM pracownicy) A,
(SELECT opis etat FROM etaty) B;
| numer | nazwisko | etat |
|---|---|---|
| 101 | Jan Nowak | cały |
| 101 | Jan Nowak | pół |
| 102 | Jan Kowalski | cały |
| 102 | Jan Kowalski | pół |
| 103 | Marek Malinowski | cały |
| 103 | Marek Malinowski | pół |
W tym przykładzie widać, że możemy podać definicję (zapytanie) relacji w miejsce relacji.
Rzut
Operacja rzutu polega na wybraniu kolumn tabeli reprezentującej relacje. Na przykład w poprzednim przykładzie z tabeli pracownicy możemy dokonaliśmy rzutu na A(numer, nazwisko) poleceniem
SELECT numer, nazwisko FROM pracownicy
Jeśli przez R oznaczymy relacje (schemat relacji), a przez r schemat rzutu tej relacji, to mówimy o rzucie relacji R na r. W naszym przykładzie chodzi o rzut „pracownicy” na „A”.
Selekcja
Operacja selekcji polega na wybraniu z relacji krotek (rekordów, wierszy) spełniających określony warunek. W SQL wykonuje się to zapytaniem SELECT z opcją WHERE ... .
Złączenie
Złączenie relacji A i B względem określonych atrybutów złączeniowych (A1, ... , Ai) i (B1, ... ,Bj) oraz wyrażenia logicznego L jest relacja o następujących własnościach:
schemat relacji jest suma schematów relacji A i B;
łączone są te krotki relacji A i B, których wartości składowych. dla atrybutów połączeniowych spełniają wyrażenie L.
Weźmy na przykład tabelę (relację) ZATRUDNIENIE:
| id | numer | data_od | data_do | aktualne | wymiar |
|---|---|---|---|---|---|
| 1 | 101 | 2016-12-31 | 0 | 0,5 | |
| 2 | 102 | 2017-01-01 | 1 | 1 | |
| 3 | 103 | 1 | 1 | ||
| 4 | 101 | 1 | 1 |
Zawiera ona informację o historii zatrudnienia pracowników - ale zawiera tylko ich numery. Chcąc wyświetlić informację o aktualnym zatrudnieniu możemy złączyć dwie relacje:
A: SELECT nazwisko, numer FROM pracownicy;
B: SELECT numer, wymiar FROM zatrudnienie WHERE aktualne>0;
Atrybut złączeniowy mamy oczywiście tylko (numer) dla obu tabel.
Wyrażenie logiczne L: A.numer = B.numer
Złączenie możemy zdefiniować w SQL na przykład tak:
SELECT A.nazwisko, A.numer, B.numer, B.wymiar FROM
(SELECT numer, nazwisko FROM pracownicy) A,
(SELECT numer, wymiar FROM zatrudnienie WHERE aktualne>0) B
WHERE A.numer = B.numer;SELECT A.nazwisko, A.numer, B.numer, B.wymiar FROM
(SELECT numer, nazwisko FROM pracownicy) A,
(SELECT numer, wymiar FROM zatrudnienie WHERE aktualne>0) B
WHERE A.numer = B.numer;
Istnieje jednak bardziej naturalny sposób – z wykorzystaniem opcji JOIN (połącz):
SELECT A.nazwisko, A.numer, B.numer, B.wymiar FROM
pracownicy A
JOIN
(SELECT numer, wymiar FROM zatrudnienie WHERE aktualne>0) B
ON A.numer = B.numer;
Jeszcze prościej (choć nie jest to zapytanie w pełni równoważne z powyższym):
SELECT A.nazwisko, A.numer, B.numer, B.wymiar FROM pracownicy A
JOIN zatrudnienie B ON A.numer = B.numer
WHERE B.aktualne>0;
W każdym przypadku otrzymamy tabelę:
| A.nazwisko | A.numer | B.numer | B.wymiar |
|---|---|---|---|
| Jan Kowalski | 102 | 102 | 1 |
| Marek Malinowski | 103 | 103 | 1 |
| Jan Nowak | 101 | 101 | 1 |
Złączenie naturalne
Jest to takie złączenie, że atrybuty złączeniowe dla obu relacji identyfikowane poprzez jednakowe nazwy, a warunek L jest koniunkcją warunków równości atrybutów o jednakowych nazwach. W przypadku z łączenia naturalnego do schematu relacji wynikowej atrybuty złączeniowe wchodzą jednokrotnie (przed złączeniem występowały dwukrotnie - w każdej z łączonych relacji).
W powyższym przykładzie chodzi o atrybut numer , który może wystąpić tylko raz.
SELECT A.nazwisko, A.numer, B.wymiar FROM
pracownicy A
JOIN
(SELECT numer, wymiar FROM zatrudnienie WHERE aktualne>0) B
ON A.numer = B.numer;
Jak zaprojektować bazę danych?
Jeśli dla tabel z powyższych przykładów zastosujemy zapytanie SQL:
select p.numer, p.nazwisko,p.pensja, z.aktualne,z.data_od,z.wymiar, e.opis etat
from pracownicy p, zatrudnienie z, etaty e
where p.numer=z.numer and e.wymiar=z.wymiar;
to uzyskamy tabelę w której znajdują się wszystkie najważniejsze informacje o pracownikach:
| numer | nazwisko | pensja | aktualne | data_od | wymiar | etat |
|---|---|---|---|---|---|---|
| 101 | Jan Nowak | 1800 | 0 | 0.5 | pół | |
| 101 | Jan Nowak | 1800 | 1 | 1 | cały | |
| 102 | Jan Kowalski | 2000 | 1 | 2017-01-01 | 1 | cały |
| 103 | Marek Malinowski | 1750 | 1 | 1 | cały |
Czy nie lepiej zapamiętać dane w takiej jednej tabeli, niż tworzyć zapytania wymagające połączeń? Problem nie jest trywialny (wymaga doświadczenia). Ale teoretycznie rzecz ujmując można znaleźć dość jednoznaczną odpowiedź. Czym grozi zastosowanie jednej tabeli? Pojawiają się problemy z których najważniejsze to redundancja i anomalie przy aktualizacji:
Redundancja – nazwisko Jan Nowak jest pamiętane w dwóch miejscach.
Anomalie przy aktualizacji - gdy zechcemy dopisać Nowakowi drugie imię – może pojawić się niejednoznaczność danych.
Ponadto mogą pojawić się (mniej oczywiste w tym przykładzie) anomalie przy wstawianiu (nie można zaplanować na przykład ¼ etatu póki nie mamy pracownika tak zatrudnionego) i usuwaniu (po usunięciu pracowników zatrudnionych na pół etatu znika informacja że jest to wymiar 0.5).
Aby tego uniknąć zaleca się projektowanie baz danych w tak zwanej trzeciej postaci normalnej. Do jej zrozumienia musimy ponownie przywołać wprowadzone już pojęcie klucza. Tabela może mieć więcej kluczy (niekoniecznie klucz główny). Możemy przyjąć, że kluczem jest minimalny zestaw atrybutów, taki że możemy jednoznacznie podzielić krotki relacji według wartości tych atrybutów. Na przykład w powyższej tabeli możemy jednoznacznie podzielić wiersze według numerów lub etatów. Dla przypomnienia – kluczem głównym jest klucz który pozwala dokonać takiego podziału w sposób funkcyjny (dla każdej wartości atrybutów klucza uzyskujemy co najwyżej jedną krotkę). Trzecia postać normalna to taki zbiór relacji, że każda z nich ma klucz główny (zauważmy, że powyższa tabela nie posiada klucza głównego) oraz żaden atrybut nie należący do tego klucza nie zależy funkcyjnie od innych atrybutów (nie należących do klucza). Pierwsza część warunku może zostać spełniona przez wprowadzenie dodatkowego atrybutu ID (od „identyfikator”). I tak często w praktyce jest to robione (dodatkowo stosuje się automatyczne zwiększanie ID przy wstawianiu nowych wierszy – tak zwany autoincrement). Jednak w takiej tabeli nazwisko zależy funkcyjnie od numeru a wymiar od etatu. Nie jest więc spełniona druga część warunku.
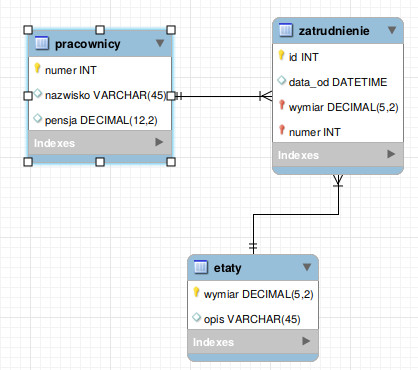
Na szczęście istnieje bardzo prosty sposób na zaprojektowanie bazy danych będącej w 3 postaci normalnej (nawet bez pełnego zrozumienia na czym ona polega). Wystarczy bazę danych zaprojektować w postaci diagramu ERD z wykorzystaniem powiązań relacyjnych (1:n) wszędzie gdzie to jest możliwe. Jest to naprawdę nietrudne, jeśli zastosujemy na przykład program MySQL Workbench (zob. opis na stronie http://reinstalacja.pl/wizualne-tworzenie-bazy-danych-mysql-jak-stworzyc-strukture-bazy-danych/).
Dla naszego przykładu diagram taki będzie wyglądał następująco: